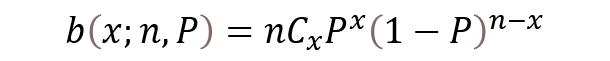Seguramente esta sea la pregunta que más se hace la humanidad desde que se desató la Covid-19. Responderla es relevante.
Desafortunadamente se trata de un tema extremadamente complejo. Sin embargo, vale la pena enfrentarse al reto de resolverlo empleando una metodología científica.
¡SÚMATE A NUESTRA COMUNIDAD!
Existen numerosos modelos epidemiológicos convencionales como el SIR o el SIRD o ecuaciones como la de Gompertz que permiten hacer predicciones muy precisas sobre la evolución de una enfermedad infecciosa. Funcionan muy bien en espacios acotados y en tiempos relativamente pequeños.
Para eso se diseñaron. Por ejemplo, en sus comienzos el modelo SIR se aplicó a la transmisión de la gripe dentro de un reputado internado británico. Sus predicciones resultaron de una exactitud asombrosa.
El éxito de estos modelos depende de estimar con la máxima exactitud una serie de parámetros (como el factor de reproducción R, el número reproductivo básico R0, la tasa de mortalidad m…) que caracterizan la evolución en el tiempo de una enfermedad infecciosa. Conocidos estos valores sabremos perfectamente como va a evolucionar una enfermedad infecciosa en los próximos días.
Desafortunadamente, estos modelos epidemiológicos clásicos no funcionan bien a la hora de hacer predicciones a largo plazo ante un problema tan complejo y diverso como es la pandemia del coronavirus. No se puede estimar con precisión los valores de los parámetros que caracterizan la infección por la Covid-19 (R, R0), sobre todo si algunos países compilan un registro de datos de infectados y muertos que se aproxima bastante bien a la realidad mientras que otros no lo hacen. Incluso la disparidad de datos reales es enorme. Por ejemplo, la tasa de mortalidad por Covid-19 en Alemania es mucho más baja que en Perú o Nicaragua.
Ante una diversidad tan extrema de parámetros epidemiológicos, los modelos convencionales no resultan fiables.
Como alternativa se están realizando predicciones sobre la pandemia mediante procedimientos de Big data y de inteligencia artificial.
La paradoja de Searle
Sin duda podrían arrojar conclusiones fiables y ser el futuro. Pero también podrían caer en la “paradoja de Searle”, como advierte a menudo el premio Nobel de física de este año Roger Penrose.
Vale la pena conocerla:
Supongamos que encierran al señor Searle, incomunicado en una pequeña habitación aislada del exterior salvo por una rendija estrecha por la que solo pueden entrar y salir papeles.
Fuera de esa habitación hay un chino al que le han dicho que dentro del cuarto hay un superordenador capaz de responder a cualquier pregunta que le haga. El chino, desconfía. Escribe una pregunta en un papel (por supuesto mediante un sinograma en chino) y la introduce por la rendija. El chino sabe la respuesta correcta a la pregunta. Solo está averiguando si es cierto que el superordenador de dentro es capaz de responderla correctamente.
Dentro de la habitación el señor Serle, que no sabe chino, ve el papel con el sinograma que entra por la rendija y no entiende absolutamente nada de lo que significa. Pero Searle tiene un libro de instrucciones escrito en su propio idioma que le indica que debe recoger el papel y observar cuidadosamente el sinograma que contiene. Después debe buscarlo en el catálogo contenido al final del libro. Cuando lo encuentre debe copiar en otro papel un nuevo sinograma que aparece justo al lado del que encontró. Cuando haya acabado de copiarlo debe colocarlo en la rendija que comunica con el exterior.
Fuera de la habitación el chino comprueba que siempre que introduce un papel con una pregunta en la rendija, al cabo de un rato sale otro papel con la respuesta correcta bien escrita en sinogramas. Tras varias pruebas exitosas por fin el chino termina creyendo que dentro de la habitación hay un superordenador capaz de responder perfectamente a sus preguntas.
Pero la realidad es que la única inteligencia que hay dentro de la habitación es el señor Searle, que no entiende absolutamente nada de lo que está pasando porque no sabe chino. Solo hace lo que le dice el libro de instrucciones sin tener ni idea de su significado.
Por fin el chino se decide. Copia en un papel el sinograma con la pregunta esencial, cuya respuesta no sabe, pero que le interesa tanto que lleva toda su vida esforzándose en resolverla. Esperanzado introduce su pregunta en la rendija.
Searle la recoge y se dispone a seguir las instrucciones. Pero le surge un problema enorme. El sinograma que está en el papel no aparece en el catálogo de su libro de instrucciones. ¿Qué hacer? Tras pensarlo un rato Searle decide pintar en un papel un sinograma que le parece bonito. Lo hace y coloca el papel en la rendija.
El chino lo contempla. Queda asombrado. Al fin conoce la respuesta a la gran pregunta que ha intentado contestar con infinito esfuerzo durante toda su vida. Se va feliz de que el superordenador haya dado la respuesta correcta a la gran cuestión que tanto le interesaba.
Por supuesto el señor Searle nunca tuvo ni la más remota idea de que había resuelto, sin fundamento alguno, la gran duda del chino.
Como advierte Roger Penrose, debemos tener cuidado. La inteligencia artificial nos podría engañar como a un chino.
Te puede interesar: ‘Ser madre en tiempos de coronavirus: Las 10 preguntas más frecuentes’
Los modelos matemáticos
Por suerte la ciencia dispone de alternativas a los modelos epidemiológicos convencionales y a la inteligencia artificial.
Se trata de elegantes modelos matemáticos de tipo Copernicano que han sido utilizados a menudo por físicos para abordar problemas intrincados. Por ejemplo, cuánto tardarán los humanos en extinguirse o cuántos humanos más nacerán antes de que lleguemos a nuestro final como especie.
Por supuesto, estos problemas sobre la duración de nuestra especie no permiten saber, a día de hoy, si los modelos Copernicanos funcionan correctamente. Pero también se han aplicado a problemas mucho más mundanos que sí permiten validar la capacidad de acierto de estos modelos.
Por ejemplo, en 1969 el astrofísico Richard Gott desarrolló un modelo Copernicano, que llamó ‘Argumento Delta-t’, para predecir cuándo caería el Muro de Berlín. Estimó que el muro aún duraría unos 20 años más, 24 como mucho. Acertó de pleno, pues el Muro de Berlín cayó en 1989.
El 17 de Mayo de 1993 Richard Gott comprobó que en la cartelera de Broadway había 44 espectáculos y predijo cuánto duraría cada uno de ellos en cartel. El tiempo demostró que su predicción había sido exacta para 42 de ellos.
Gott desarrolló su modelo predictivo de ‘Argumento Delta-t’ siguiendo el “principio Copernicano” y el “principio de mediocridad”.
Se trata de un razonamiento de teoría de probabilidades muy simple, pero extremadamente poderoso. Como solo somos observadores mediocres de un acontecimiento cualquiera que y no ocupamos ninguna posición privilegiada en el tiempo, lo más probable es que cualquier cosa seleccionada al azar que observemos en un momento determinado no esté ni al comienzo ni al final de su vida. Más bien estará en algún punto situado a un lado u otro de la mitad de su vida.
Esta idea intuitiva se puede formalizar matemáticamente en forma de una desigualdad que permite estimar cuánto más va a durar un evento. Por ejemplo, la actual pandemia de coronavirus. (Para quienes tengan interés matemático, describimos la desigualdad de Gott en una adenda al final del artículo.)
Las predicciones basadas en metodologías Copernicanas como el ‘Argumento Delta-t’, el Principio del Juicio Final, la Catástrofe de Carter o la Ley de Lindy, son idóneas para predecir fenómenos muy complejos caracterizados por su gran incertidumbre, en los que la dinámica temporal es uno de los datos más fiables que pueden conseguirse. La Covid-19 es un buen ejemplo.
Por eso las predicciones sobre la duración de la Covid-19 basadas en el argumento Delta-t resultan muy interesantes. Así el 6 de Agosto de 2020 se publicó un artículo utilizando el argumento Delta-t y otros modelos Copernicanos estimando que la pandemia de coronavirus podría controlarse a nivel mundial hacia finales de 2022, y en el peor de los casos durante 2024.
Esto por sí solo es un avance. Pero hay 194 países en el mundo y sin duda unos lograrán controlar la pandemia antes que otros. Es más interesante predecir en que fechas los distintos países conseguirán controlar la pandemia.
Pero claro, esto complica el modelo predictivo.
El argumento Delta-t, otros procedimientos Copernicanos y del principio de mediocridad no bastan por sí solos para hacer predicciones sobre la duración de la pandemia en los distintos países.
Pero es posible completar el argumento Delta-t con otros procedimientos de probabilidad para obtener un modelo predictivo adecuado que sea aplicable para ‘conocer’ la duración de la pandemia en los 194 países del mundo.
Dos escenarios diferentes
Para ello tenemos que contemplar dos escenarios diferentes bien caracterizados en una parte de las matemáticas llamada la teoría de juegos.
– En el primer caso los países no cooperan entre sí. Cada uno se apaña por sí mismo como puede en la lucha contra la pandemia.
– En el segundo de los escenarios, los distintos países colaboran en mayor o menor grado. Este es un escenario mucho más realista. Un ejemplo: si un país desarrolla una vacuna es altamente probable que no se limite a utilizarla exclusivamente en su propio territorio, sino que intentará vendérsela a otros.
Empecemos considerando el primero de los casos (los países no cooperan entre sí).
El argumento Delta-t nos permite calcular un intervalo de tiempo en el que se empezará a controlar la Covid-19. Este intervalo de tiempo estaría entre Mayo de 2021 y Diciembre de 2023.
En realidad, algunos países conseguirían controlar la pandemia de Covid-19 hacia el verano próximo. Otros tardarían más y lo irían logrando hacia finales de 2021. Habría países que lo harían durante 2022. A los que peor les fuese terminarían por conseguirlo durante 2023. Muy pocos tardarían más.
La teoría estadística, concretamente el teorema central del límite, nos dice que en el caso de que los distintos países no colaborasen entre sí (son por tanto variables independientes), la distribución de las fechas en que conseguiría controlar la pandemia de Covid-19 se aproximan bien a una distribución de probabilidad normal (los que tengan interés matemático, pueden consultar la adenda al final del artículo).
En la práctica, la combinación del argumento Delta-t de Gott con el teorema del límite central predice que entre 4 y 5 países conseguirán librarse de la Covid-19 antes del 30 de Septiembre de 2021. Otros 26 países lo conseguirán entre Octubre de 2021 y final de Febrero de 2022. La mayoría de los países (alrededor de 132) se librarán del coronavirus entre Marzo y Diciembre de 2022. Los restantes lo irán consiguiendo durante 2023. Como mucho uno o dos países tardarían más.
Recordemos que esto se cumplirá solo en el caso de que los distintos países no cooperen entre sí.
Consideremos ahora el caso más realista de que los distintos países cooperan en mayor o menor grado entre sí.
En función de su desarrollo científico y sanitario podemos encontrar distintos tipos de países.
– En un extremo estarían los que son capaces de salir adelante por sus propios medios de manera rápida (pueden fabricar y desarrollar vacunas y fármacos eficaces y cuentan con la capacidad logística para implementar estrategias de control y de vacunación efectivas).
– Otros países no desarrollan vacunas ni fármacos rápidamente, pero tienen recursos suficientes para comprarlas y medios para usarlas de manera eficiente.
– Un tercer grupo incluye a aquellos países que no pueden comprar vacunas ni fármacos caros, pero tienen infraestructura para aplicar eficientemente cualquier ayuda internacional que puedan recibir.
– Por último, tendríamos países sin la suficiente logística como para utilizar eficientemente la ayuda internacional.
Considerando las condiciones de contorno de este modelo de estrategia corporativa que aseguren que el mejor resultado posible (es decir, tiempo mínimo necesario para que los diferentes tipos de países controlen la pandemia de COVID-19) podemos estimar la distribución temporal de las fechas en las que los diferentes países estarán libres de COVID-19, utilizando una distribución de probabilidad binomial. (Los que sientan interés matemático pueden consultar la adenda al final del artículo.)
En la práctica consideramos que aquellos países que disponen de menos de 100 dólares por persona y año para gastos sanitarios no contarán con la logística necesaria para aprovechar la colaboración internacional. En estos momentos el 41,7% de los países del mundo se encuentran en esta situación.
Con estas asunciones este modelo predice que:
– sólo 38 países conseguirán librarse de la Covid-19 antes del 30 de Septiembre de 2021.
– La mayoría de los países, 82 en total, se librarán de la pandemia de coronavirus entre Octubre de 2021 y finales de Abril de 2022.
– Alrededor de 59 países más se librarán de la Covid-19 entre mayo y Noviembre de 2022.
– Apenas un par de países tardarán más en hacerlo.
Insistimos una vez más en que las estimaciones de este modelo están hechas con las condiciones de contorno mejores. Estas previsiones son lo mejor que nos puede pasar.
España debería estar entre los países del segundo grupo y podríamos conseguir librarnos de la Covid-19 entre Octubre de 2021 y Abril de 2022.
Pero el proceso de librarnos de la Covid-19 será gradual y no ocurrirá como un milagro de un día para otro. Poco a poco iremos aumentando el porcentaje de población inmunizada frente al SARS-CoV-2, conseguiremos que los contagios no sigan descontrolados, tendremos mejores protocolos, etc., hasta conseguir que los casos de Covid-19 sean marginales.
Tampoco podremos bajar la guardia. Hay muchos indicios de que este coronavirus ha venido para quedarse. Con él pasará lo mismo que con el sarampión o la polio. Probablemente no será pandémico, pero se darán casos especialmente entre los grupos anti-vacunas, tal y como ocurre ahora con otras enfermedades infecciosas.
Por último, debemos destacar que la comparación de ambos modelos (estrategia de cooperación frente a estrategia de no cooperación) muestra la importancia de la cooperación internacional. Un modelo fuertemente cooperativo predice que la pandemia de COVID-19 podrá estar razonablemente bajo control para noviembre de 2022, lo que permitiría volver a la vida normal en todo el mundo. Sin esa cooperación será necesario otro año más.
Está claro que la pandemia de COVID-19 no es solo un problema médico o científico, sino que tiene implicaciones económicas, políticas y sociales que hacen muy difíciles las predicciones.
Addenda para los aficionados a las matemáticas:
Un poco de aderezo de sal y pimienta matemáticas
Un evento copernicano cualquiera se distribuye en el tiempo con 3 momentos característicos:

Considerando nuestra posición como no privilegiada, cualquier evento observable solo puede medirse entre su tiempo de inicio (ti) y su tiempo final (tf). Si estamos en un momento no privilegiado en el tiempo, podemos asumir que nuestro tiempo actual (ta) estará aleatoriamente en algún punto de la duración del total del evento. Para eso la razón r = (ta-ti) ⁄ (tf-ta) es un número entre 0 y 1.
De esta manera, se cumplirá que:
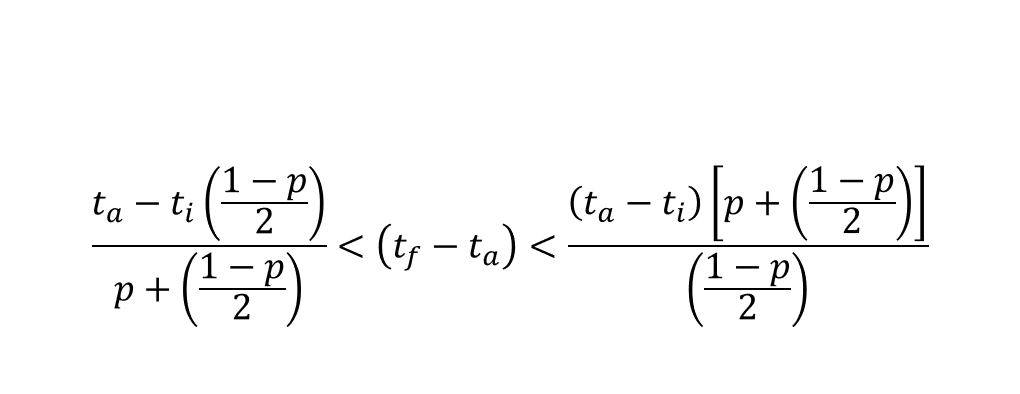
Esto es la desigualdad de Gott y permite estimar la duración de un evento copernicano.
Además de esta desigualdad, en el modelo no cooperativo también empleamos la función de distribución acumulativa del teorema del límite central:
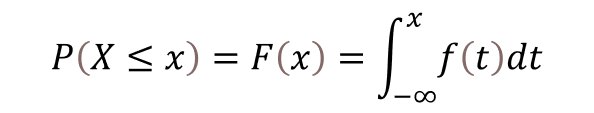
mientras que en el modelo cooperativo utilizamos la distribución de probabilidad binomial: